도구변수법은 현재 계량경제학의 꽃으로, 관측 불가능한 변수까지 통제할 수 있는 아주 좋은 방법이다. 영어로는 Instrument Variable Method, 줄어야 IV방법이라고 칭한다. 관측 불가능한 변수까지 통제하는 것이 좋은 이유는, 관측불가능한 변수로 인한 생략변수편향(bias)문제를 해결할 수 있기 때문이다. 그러나 IV를 사용하기 위해서는 약간의 조건도 있다. 바로, 창의력이 필요하다는 것이다. 왜 그런지는 아래에서 다른 설명과 함께 서술하겠다.
도구변수에 대해 간단하게 정의하자면, 관심변수와 관련있지만 오차항과는 관련이 없는 변수다. 조금 풀어서 설명하면, 관심변수에 대한 실제 데이터를 사용하는 것이 아니라, 관심변수를 설명할 수 있으면서 다른 변수들과는 상관이 없는 변수를 통해 추정한 관심변수의 추정값을 사용하는 것이다. 이 값은 다른 변수들과 상관이 없으므로 다른 변수들을 생략해도 편향이 일어나지 않게 된다.
예를 들어 설명하기에 앞서, IV방법의 단계를 설명하면 다음과 같다.

First stage에서는 관심변수(D)를 도구변수(Z)에 대해 OLS한다. 이렇게 얻은 절편 추정치(a)와 계수 추정치(bz)를 통해 D를 추정하게 된다. 이렇게 추정한 D를 Second Stage에서 실제 D 대신 넣고 OLS한다. 이렇게 얻은 계수 추정치(b1)는 불편성을 가지게 된다.
한편, Reduced form을 통해 제대로 구한 것이 맞는지 검증할 수 있다. 먼저, 위의 방법을 통해 얻은 추정치 b1을 아래와 같이 정의할 수 있다.

즉, Second Stage에서 얻은 값과 Reduced Form에서 얻은 값을 First stage에서 얻은 값으로 나눈 값이 일치한다면, 제대로 된 것이다. 그러나 이렇게 얻은 값이 인과성을 가지기 위해서는 다음의 IV의 두 가지 가정을 만족해야한다.
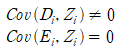
첫번째는 관심변수(D)와 도구변수(Z)가 상관관계를 가져야한다는 것이고, 두번째는 Second Stage의 오차항(E)과 도구변수(Z)가 독립임을 의미한다. 관심변수와 도구변수가 상관관계를 가져야 하는 이유는 설명하지 않아도 될 것이다. 그렇다면 오차항과 도구변수가 독립이어야 하는 이유는? 그래야 편향되지 않은 값을 얻을 수 있기 때문이다. 만약 상관이 있다면 도구변수를 활용하는 이유가 없어진다. 여기서 창의력이 필요한 이유를 알 수 있다. 이 두 조건을 만족하는 도구변수를 찾는 것이 매우 어렵기 때문이다.
Yutaro Izumi의 논문을 예시로 들면1, 3.1운동의 유무가 그 지역의 초등학교 수에 미친 영향을 밝히고자 하였다. 쉽게 이야기하면 일제가 3.1운동의 보복으로 초등학교를 닫았는지, 혹은 초등학교 수를 늘려서 불만을 잠재우고자했는지 파악하려고 하였다. 그러나 문제는 시민의식이다. 어느 지역의 시민의식이 높으면 3.1운동이 해당 지역에서 벌어졌을 확률이 높아질 것인데, 시민의식이 높으면 초등학교 수가 많을 가능성도 높아질 수 있다. 그런데 이러한 시민의식은 측정이 불가능하다. 따라서 저자는 도구변수를 활용하였는데, 바로 3.1운동 즈음의 지역별 강수량을 사용했다. 강수량이 많으면 3.1운동이 취소되었을 확률이 높고(1번 가정 충족), 시민의식 등과는 관련이 없다(2번 가정 충족). 이런 식으로 어찌보면 뚱딴지같은 변수를 가져와야하기 때문에 창의력이 필요하다.
이러한 도구변수법을 사용할 때는 약한 도구 세팅(Weak Instruments Setting)으로 인한 유한샘플편의(Finite-Sample Bias)를 조심해야한다. 약한 도구 세팅이란 IV의 두 가지 가정을 만족하긴 하지만 그 정도가 약한 것으로, 관심변수와 도구변수 간 상관관계가 약한 것을 의미한다. Finite-Sample Bias는 쉽게 설명하면 IV방법을 통해 추정한 계수가 실제 모수와 차이가 큰 것이다. 관심변수와 도구변수의 상관관계가 약하다면 First Stage에서 추정한 관심변수의 추정치는 정확하다고 하기 어렵다. 이러한 정확한지 모르겠는 값을 사용하여 얻은 관심변수의 계수 추정치는 당연히 정확하다고 하기 어려울 것이다. 그렇다면 상관관계가 강하다는 기준은 무엇일까? 일반적으로 First Stage의 F통계량을 사용한다. F값이 10 이상일때, 충분한 상관관계를 가진다고 경험적으로 판단하게 된다.
한편, 논문을 쓸 때, 오차항과 도구변수가 서로 독립이라는 것에 대한 통계적인 방법은 없다. 따라서 충분한 선행연구의 제시를 통해 설득해야 한다.
이처럼 완벽해보이는 방법이지만 당연히 한계도 있다. 도구변수법을 사용한 논문의 한계로 적기도 하는 내용으로, IV의 단조성 가정(Monotonicity Assumption)이다. 이는 앞선 Izumi의 논문을 예시로 들면, 비가 엄청나게 쏟아지더라도 3.1운동을 진행한 지역의 데이터는 무시된다는 의미다. 따라서 IV방법을 통해 얻은 계수 추정치는 Average Treatment Effect라고 할 수 없다. ATE라고 하기 위해서는 순응자와 비순응자를 합친 전체의 평균이어야 한다. IV는 비순응자를 제외한 결과일 뿐이다.
- 계량경제학 수업 시간에 예시로 들은 것이라 제목을 모른다 [본문으로]
'NASAN's Study > 통계방법론과 프로그램' 카테고리의 다른 글
| 표준오차(S.E; Standard Errors), 로버트의 표준오차(Roberts Standard Errors), 클러스터 표준오차(Cluster Standard Errors) (1) | 2023.12.11 |
|---|---|
| 변수의 내생성(Endogeneity) (1) | 2023.11.27 |
| t통계량(t-statistic)과 t검정(t-test) (0) | 2023.11.27 |
| 통제집단합성법(SCM; Synthetic Control Method) in STATA (0) | 2023.11.16 |
| 도구변수(IV; Instrument Variable) 분석하기 in STATA (0) | 2023.11.11 |

