본 글에서는 유의확률과 관련된 개념인 t-통계량, t값, t-test에 대해 설명하고자 한다.
설명에 앞서, OLS 회귀분석을 위한 중요한 전제 중 하나인 '오차항의 등분산성 가정'을 짚고 넘어가야 한다. 오차항의 분산이 동일하다고 가정하는 이유는 오차항이 정규분포를 가져야 OLS를 통해 추정한 추정치 b가 정규분포를 따르기 때문이다. 추정치 b의 분포는 다음과 같이 표현할 수 있다.

신뢰구간을 확인하고 유의확률을 알기 위해서는 표준정규분포로 바꿀 필요가 있다. 왜냐하면 모수 b를 알 수 없기 때문이다. 또한 뒤에 다시 언급하겠지만 유의확률을 위한 귀무가설은 b=0이다. 그런데 위 식은 추정치 b만을 다루고 있으므로 계산 자체가 불가능하다. 따라서 위 식을 표준정규분포로 바꾸면 아래와 같이 나타낼 수 있다. (표준정규분포에 대한 자세한 설명은 해당 글에서 하겠다.)
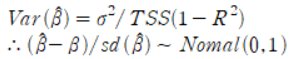
TSS는 X에 대한 Y의 관측치에서 Y평균을 뺀 값이다. sd는 표준편차로, Var(b)에 루트를 씌운 값이다. 물론 식을 그대로 신뢰도를 구하는 데 사용할 수 없다. 왜냐하면 모분산과 모표준편차를 모르기때문이다. 우리는 오로지 이에 대한 추정만이 가능할 뿐이다. 이에 따라 t분포는 다음과 같이 정의된다.
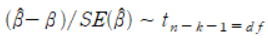
n-k-1은 자유도를 의미한다. 자유도는 자료에 따라 n-k로 표기하기도 하는데, 이 경우에는 k에 -1이 포함된 것으로, 같은 말이다. 자유도 k는 설명변수의 수를 의미한다. -1을 하는 이유는 절편도 계산 과정에서 추정되므로 일종의 변수로 볼 수 있기 때문이다. SE는 표준오차(Standard Error)로, 자세한 설명은 해당 글에서 하겠다.
이제 추정치를 이용해 t값을 얻을 수 있다. t값은 다음과 같이 정의된다.
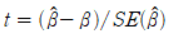
그런데 설명했듯, 모수는 그 누구도 알 수 없다. 따라서 보통은 H0: b=0이라는 귀무가설이 옳은지 그른지를 테스트하게 된다. 즉, 위 식에 b=0을 대입하면 추정치만 남으므로 계산이 가능해진다. 다시 말하면 분자가 0에 가까울수록 t값은 0에 가까워진다. 그런데 베타 추정치가 0이라는 것은 X가 Y에 영향을 미치지 않는다는 의미일 것이다. X가 아무리 변해도 Y값에 미치는 영향력은 0이기 때문이다. 여기서 t-test는 X가 영향력을 갖는지 아닌지를 모수와 추정치의 차이를 이용해 확인하는 테스트임을 알 수 있다. 추정치 b의 절댓값이 클 수록, 표준오차가 작을수록 귀무가설을 기각할 확률이 높다는 사실 또한 알 수 있다.
조금 더 쉽게 설명하기 위해 아래와 같은 회귀식을 가정하자.

b1이 0.1이고 b2가 3이면서 표준오차는 두 변수에서 똑같이 1이라고 가정하자. 변수 1과 2가 y에 정말로 영향력을 미치는지 확인하기 위해서는 t검정을 시행할 수 있다. 이때 귀무가설은 "영향력이 없다"이다. t검정을 위한 t통계량은 변수 1이 0.1, 변수 2가 3으로 나타날 것이다. 이때, t통계량은 클 수록 귀무가설을 기각할 확률이 높으므로 변수 2의 유의확률이 더 좋게 나타날 것임을 알 수 있다. 그렇다면 유의한지 아닌지는 어떻게 알 수 있을까?
다행히도 직접 계산할 필요는 없고, 임계치를 나타낸 표가 있다. 만약 5%(=0.05)유의수준에서 귀무가설 기각을 하기 위해서는 t값의 절댓값이 임계치의 절댓값보다 커야 한다. 아래 예시는 양측검정의 경우인데, 1.96보다 t통계량의 절댓값이 크면 귀무가설을 기각하게 된다. 각 임계치가 나타난 표는 제시하지 않겠다. (검색하면 나온다.)

추가적으로 설명하자면, 추정치 b의 절댓값이 클수록 귀무가설을 기각한다는 것은, 생략변수편향이 일어났을 때 계수가 과대 혹은 과소추정되면 정확한 추정치는 귀무가설을 기각하지 못하더라도 편향된 추정치는 귀무가설을 기각할 수도 있다는 것이다. 논문 작성 시, 여러 모델을 사용하게 되면 A모델에서는 유의하지 않았는데 왜 B모델에서 유의하게 나왔는지 설명하라는 심사의견이 종종 오곤 한다. 이럴 때 t통계량과 t테스트를 이해하고 있으면 관련해서 답변을 작성할 수 있다.
또한 표준오차 설명글에서 자세히 설명하겠지만, N이 커지면 표준오차가 작아지는 문제가 발생한다. 즉, N이 커질수록 t통계량의 분모가 작아지기 때문에 t값이 커진다. t값이 커지면 귀무가설을 기각하기 쉬워진다. 따라서 일반적인 표준오차 대신 Robust Standard Errors나 Cluster Standard Errors를 많이 이용한다.
'NASAN's Study > 통계방법론과 프로그램' 카테고리의 다른 글
| 표준오차(S.E; Standard Errors), 로버트의 표준오차(Roberts Standard Errors), 클러스터 표준오차(Cluster Standard Errors) (1) | 2023.12.11 |
|---|---|
| 변수의 내생성(Endogeneity) (1) | 2023.11.27 |
| 통제집단합성법(SCM; Synthetic Control Method) in STATA (0) | 2023.11.16 |
| 도구변수(IV; Instrument Variable) 분석하기 in STATA (0) | 2023.11.11 |
| 탐색적요인분석(EFA; Exploratory Factor Analysis) (1) | 2023.11.04 |

